Navigation: Home=>Profil=>Antriebstechnik=>Patent=>Bechreibung  Stand: 08.05.1999

Der Motor 1 bewegt die Last 2, deren Lage geregelt werden soll. Die tatsächliche Lage der Last 2 wird mit einer Positionsmessung 3, z.B. durch einen inkrementalen Drehgeber, festgestellt und als Regelgröße 4 an den Regler 5 gemeldet. Aufgabe des Systems ist es, die Regelgröße 4 (= Lage-Istwert = Sist) schnell und exakt auf die Führungsgröße Lage-Sollwert ( = Zielposition = Ssoll) einzustellen, die dem Regler 5 von dem äußeren Leitsystem 7 vorgegeben ist. Der Regler 5 bildet dazu die Stellgröße 8 in Form eines Wertes für den Motorstrom 9. Der entsprechende Motorstrom wird dem Motor 1 vom Leistungsverstärker 10 eingeprägt. Er bewirkt ein Drehmoment an der Motor-Achse und damit eine Beschleunigung der Last 2, die die Last 2 in die Zielposition verschiebt.

Neben dem Lage-Sollwert kann dem Regler 5 als zweite Führungssgröße ein Geschwindigkeits-Sollwert 11 (Vsoll) vorgegeben werden. Die Last 2 erreicht das Ziel dann mit der gewünschten Geschwindigkeit. Auf diese Weise lassen sich beliebige Bahnkurven (Ssoll = f (t) und Vsoll = f ' (t)) abfahren, indem der Regler 5 eine ununterbrochene Folge von Stützpunkten der Bahnkurve ansteuert.

Derartige Regelkreise sind Stand der Technik (z.B. Ludwig Merz et al.: Grundkurs der Regelungstechnik, 9. Auflage, R. Oldenbourg Verlag, 1988, S. 268 und Hans-Jürgen Schaad: Praxis der digitalen Antriebsregelung, Franzis-Verlag, 1992, S. 17). Konventionell werden dazu PD- oder PID-Regler eingesetzt, die teilweise mehrfach ineinander verschachtelt sind (Kaskadenregelung). Jedoch neigen diese Regelungen entweder zum Überschwingen in der Zielposition oder die Last schleicht zu langsam an die Zielposition heran, was zu langen Ausregelzeiten führt. Das Zeitverhalten kann zwar mit dem Verfahren aus der US 4694229 verbessert werden, aber bei allen bekannten Reglern ist der Ankunftszeitpunkt nicht genau vorhersagbar und die Ankunft kann sich verzögern, falls externe Störeinflüsse auf den Bewegungsablauf einwirken. Außerdem bewirkt die Regelcharakteristik einen unnötig hohen Energieverlust des Motors.

Der Erfindung liegt die Aufgabe zugrunde, ein Regelungsverfahren zu entwickeln, das die obengenannten Nachteile vermeidet und das als genau, schnell, stabil, überschwingungsfrei, robust, energiesparend und einfach charakterisiert werden kann. Die Aufgabe wird durch die Lehre der Patentansprüche gelöst.

Bei der Diskussion der Regeleigenschaften wird auf die Figuren 2 bis 14 Bezug genommen. Sie zeigen exemplarisch den zeitlichen Verlauf der drei Größen Motorstrom (IMotor), Last-Geschwindigkeit (Vist) und Entfernung der Last vom Ziel (Sist - Ssoll) unter verschiedenen Betriebsbedingungen:

Figur  2: Neues Regelprinzip unter idealen Bedingungen
Figur  3: Dreiecksförmiges Geschwindigkeitsprofil
Figur  4: Verlauf bei negativer Anfangsgeschwindigkeit
Figur  5: Verlauf bei positiver Anfangsgeschwindigkeit
Figur  6: Konstante "Trägheit" ist 33% zu hoch eingestellt
Figur  7: Konstante "Trägheit" ist 33% zu niedrig eingestellt
Figur  8: Geschwindigkeit durch externe Einflüsse gestört
Figur  9: Die Lage wird durch externe Einflüsse gestört
Figur 10: Vom Stillstand zu einer positiven Endgeschwindigkeit
Figur 11: Identische Anfangs- und Endgeschwindigkeit
Figur 12: Verlauf bei negativer Endgeschwindigkeit
Figur 13: Konstante Beschleunigung gemäß Gleichung (11)
Figur 14: Linear abnehmende Beschleunigung nach Gleichung(12)

Ausgangspunkt ist die bekannte physikalische Erkenntnis, daß sich die Geschwindigkeit eines Körpers aus dem Integral der Beschleunigung ergibt und daß das Integral der Geschwindigkeit den zurückgelegten Weg beschreibt. Aus diesen Naturgesetzen der Bewegungslehre lassen sich zwei Bedingungen für den Verlauf der Beschleunigung der Last aLast(t) formulieren, die erfüllt sein müssen, damit das Regelungsziel (Ssoll, Vsoll) bei Ablauf der Ausregelzeit ta tatsächlich erreicht wird:

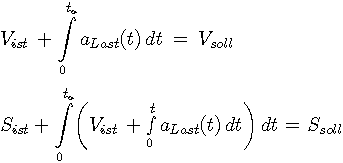(1)       (2)

Es bedeuten:
ta=         Ausregelzeit bis zum Erreichen der Zielposition [s]
aLast=    Beschleunigung der Last [m/s²]
Vist=      Geschwindigkeits-Istwert [m/s] = Start-Geschwindigkeit (zum Zeitpunkt t = 0)
Vsoll=     Geschwindigkeits-Sollwert [m/s] (zum Zeitpunkt t = ta)
Sist=       Lage-Istwert [m] = Start-Position (zum Zeitpunkt t = 0)
Ssoll=      Lage-Sollwert [m] = Zielposition (zum Zeitpunkt t = ta)

Wie durch Einsetzen von (3) in (1) und (2) nachgeprüft werden kann, wurde mit der folgenden Geradengleichung (3) eine Funktion für aLast(t) gefunden, die beide Gleichungen (1) und (2) erfüllt:

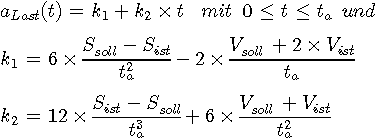(3)   (3a) (3b)

Der lineare Verlauf der Beschleunigung ist vorteilhaft für den Energieverbrauch des Motors (s.u.) und führt zu einem relativ einfachen Regelalgorithmus zur Berechnung des Motorstromes. Es können aber auch Varianten dieser Gleichung mit Funktionen höherer Ordnung benutzt werden, wenn sie gleichfalls die Bewegungsgleichungen (1) und (2) einhalten. Um nach diesem Verfahren die Last-Beschleunigung aLast zu bestimmen, ist die Kenntnis der Ausregelzeit ta erforderlich. ta gibt die Zeit an, die das System für den laufenden Regelvorgang bis zum Erreichen der Zielposition benötigen wird. Wesentliches Element des neuen Reglers ist daher ein Zeit-Register (vgl. 12 in Figur 1), das den Wert ta für die Berechnung bereitstellt. Sobald das Leitsystem eine neue Zielposition vorgibt, ist das Zeit-Register zu initialisieren. Dafür bestehen grundsätzlich zwei Möglichkeiten:

a) ta wird als Bestandteil der Führungsgrößen vom Leitsystem vorgegeben (vgl. Figur 1, Schalterstellung "a"). Dies ist dann empfehlenswert, wenn das Leitsystem den Zeitpunkt kennt, zu dem die Last die Zielposition eingenommen haben soll, z.B. bei Maschinen, die einem bestimmten Arbeitstakt unterworfen sind. So kann bei einem mehrachsigen Roboter für alle Achsen der gleiche Wert für ta vorgegeben werden. Achsen, die nur einen relativ kurzen Weg zurückzulegen haben, führen die Bewegung dann entsprechend sanft aus, d.h. ruckfrei, verschleißarm und energiesparend.

b) ta wird vom Regler automatisch bestimmt (vgl. Figur 1, Schalterstellung "b"). Dieses Vorgehen empfiehlt sich, falls die Zielposition schnellstmöglich erreicht werden soll oder falls ein herkömmlicher Regler (z.B. PD-Regler) ersetzt werden soll und das Leitsystem deshalb für die Mitteilung der Ankunftszeit ta nicht vorbereitet ist.

Werden für die Beschleunigung der Last aLast (bzw. für den Motorstrom IMotor vgl. Gleichung (5)) die zulässigen Maximalwerte angenommen, so läßt sich durch Umstellen der Gleichung (3) errechnen, welche Ausregelzeit ta für den Bewegungsablauf mindestens erforderlich ist. Die Betrachtung braucht nur für t=0 und t=ta geführt zu werden, da aufgrund des linearen Verlaufes der Beschleunigung das Maximum der Beschleunigung nur an einem der beiden Endpunkte der Bewegung auftreten kann. Es ergeben sich zwei quadratische Gleichungen, deren Lösungen den zulässigen Wertebereich für ta eingrenzen. Von diesen Lösungen ist der kleinstmögliche Wert für ta zu wählen, der noch gewährleistet, daß dem System nur Beschleunigungen innerhalb seiner physikalischen Grenzen (z.B. maximales Motor-Drehmoment) abverlangt werden.

(4)

(5)

Dieser einfache, proportionale Zusammenhang gilt in guter Näherung für das in Figur 1 gezeigte System. Bei anderen Anwendungen, bei denen z.B. Reibungs-, Feder- oder Gewichtskräfte erheblichen Einfluß ausüben oder bei denen eine nicht-lineare Motorkennlinie kompensiert werden muß, ist die Gleichung (5) dementsprechend anzupassen. Der Regler muß die Gleichungen (4) und (5) in Echtzeit andauernd neu bewerten und die Stellgröße IMotor dadurch laufend aktualisieren. Er kann beispielsweise durch einen Mikrocomputer realisiert werden, der diesen Regelalgorithmus zyklisch oder periodisch ausführt. Dabei wird der eigentlich kontinuierliche Verlauf der Stellgröße durch einen zeit-diskreten, treppenförmigen Verlauf angenähert. Die Annäherung gelingt umso besser, je häufiger die Berechnung wiederholt wird. Damit keine Abweichung vom idealen Verlauf spürbar wird, sollte eine systemspezifische Zykluszeit (z.B. 500 µs) nicht überschritten werden.

Da die Ausregelzeit ta fortwährend automatisch vermindert wird, und da für jede neue Berechnung die augenblicklichen Meßwerte der Regelgrößen (Sist, Vist) benutzt werden, scheint sich der Regler stets am Anfang des Bewegungsablaufes zu befinden (t=0 im Sinne der Gleichungen (1) bis (3)), und es kann immer mit Gleichung (4) gerechnet werden. Die Gleichungen (1) bis (3) dienen nur zur Erläuterung der Zusammenhänge und werden vom Regler zur Bestimmung des Motorstromes IMotor nicht benötigt.

Gleichung (4) enthält für ta=0 eine Polstelle. In Verbindung mit Verzögerungszeiten im Regelkreis (u.a. hervorgerufen durch eine Totzeit des Leistungsverstärkers, die Induktivität des Motors und die Rechenzeit für den Regelalgorithmus) entsteht für sehr kleine Werte von ta eine Instabilität. Deshalb sollte ta nicht ganz bis auf null vermindert werden. Soll die Last im Ziel stillstehen (Vsoll=0), kann ta auf einen geeigneten Mindestwert begrenzt werden. In der Praxis hat sich bewährt, etwa den vierfachen Wert der genannten Verzögerungszeiten zu benutzen. Die Zielposition wird dann nach einer sehr kurzen Beruhigungszeit sicher erreicht. Die Verzögerungszeiten sollten so klein wie möglich gehalten werden, damit ein niedriger Mindestwert verwendet wird und die Regelung eine hohe Steifigkeit in der Endlage erzielt. Falls die Bewegung Teil einer Bahnkurve ist und die Last die Zielposition kreuzen soll (Vsoll#0), kann bereits kurz vor Erreichen des Zieles auf das nächste Segment der Bahnkurve weitergeschaltet werden.

Figur 2 veranschaulicht die Auswirkungen des Regel-Prinzips, indem der zeitliche Verlauf der drei Größen Motor-Strom (IMotor), Geschwindigkeit (Vist) und Positionsfehler (Sist - Ssoll) grafisch dargestellt wird. Bei dem gezeigten Beispiel soll die Last aus dem Stillstand um einen bestimmten Weg verfahren werden und im Ziel wiederum stillstehen (Vsoll=0). Der Regelalgorithmus führt erwartungsgemäß zu einem linearen zeitlichen Verlauf des Motor-Stromes IMotor (s. Gleichung (3)).

Man erkennt, daß die Bewegung symmetrisch zum Mittelpunkt (ta/2) verläuft. Während der ersten Hälfte der Bewegung wird die Last beschleunigt und während der zweiten Hälfte genauso wieder abgebremst.

Für herkömmliche PD- und PID-Regler sind hohe Regelgeschwindigkeit und gute Dämpfung gegenläufige Forderungen, für die durch Einstellung der Regelparameter ein Kompromiß gefunden werden muß. Das neue Regelprinzip vereint beide Forderungen. Der Regelalgorithmus erzwingt, daß die Wegdifferenz (Sist - Ssoll) und die Geschwindigkeit Vist zum Zeitpunkt des Ablaufes von ta gleichzeitig verschwinden. Die Last steht daher in der Zielposition still und ein Überschwingen kann nicht auftreten.

Der lineare Verlauf des Motorstromes hat den Vorteil, daß die Verlustleistung des Motors minimiert wird. Dies wird anhand der folgenden Berechnung verdeutlicht. Sie beruht auf der Voraussetzung, daß die Verlustleistung durch den Wicklungswiderstand R des Motors bestimmt wird ( P(t) = R x I² (t) ). Gegenüber einem dreiecksförmigen Geschwindigkeitsprofil, wie es bisher in der Technik oft angestrebt wird (vgl. Figur 3), ergibt sich eine Energieeinsparung in Höhe von 25% (vgl. Relation der Gleichungen (8) und (7)). Entsprechend kleiner kann der Motor dimensioniert werden. Anhand der Bewegungsgleichung (2) läßt sich zeigen, daß das parabelförmige Geschwindigkeitsprofil (gemäß Figur 2) gegenüber dem dreiecksförmigen Geschwindigkeitsprofil (gemäß Figur 3) zu Beginn den 1,5-fachen Motorstrom erfordert, damit in beiden Fällen nach derselben Ausregelzeit eine gleichgroße Strecke zurückgelegt wird. Somit beträgt der Energieverlust:

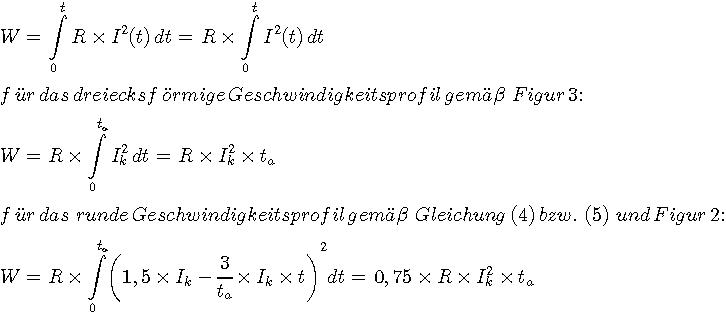(6)         (7)           (8)

Es bedeuten:
W=    Energieverlust [Ws]
R=    Motor-Wicklungswiderstand [Ohm]
Ik=   Betrag des Motorstromes beim dreiecksförmigen Geschwindigkeitsprofil gemäß Figur 3 [A]
ta=   Ausregelzeit bis zum Erreichen der Zielposition [s]

Die folgenden Beispiele belegen, daß die Regelung auch bei Abweichungen von den idealen Bedingungen prompt, angemessen und stabil reagiert:

a) Wenn die Last bei Beginn der Regelung in Bewegung ist (Figuren 4 und 5), verläuft die Stromkurve wiederum linear, allerdings nicht mehr symmetrisch zum Mittelpunkt. Die wichtige Eigenschaft, daß die Last mit Ablauf von ta in der Zielposition zum Stehen kommt, bleibt erhalten.

b)  Wenn der Regler eine Trägheit benutzt, die von der tatsächlichen abweicht (Figuren 6 und 7), wird dies in weiten Bereichen toleriert, so daß die punktgenaue Ankunft zum richtigen Zeitpunkt gewährleistet bleibt. Nachteilig wirkt sich die aufgrund der gekrümmten Motor-Stromkurve etwas erhöhte Verlustleistung aus. Anhand des konvexen bzw. konkaven Verlaufes der Stromkurve kann jedoch erkannt werden, daß mit einer fehlerhaften Trägheit gerechnet wird. Da die Trägheit das Verhältnis zwischen dem Motorstrom IMotor und der Last-Beschleunigung aLast=dVist/dt angibt (vgl. Gleichung (5)), läßt sich die Trägheit im laufenden Regelbetrieb ausmessen (Trägheit= IMotor x dt/dVist). Es ist daher leicht möglich, die Regler-Software so zu erweitern, daß sich der Regler auf den optimalen Wert für die Trägheit automatisch einstellt

Die Trägheit ist der einzige verstellbare Regelungsparameter. Demgegenüber müssen bei herkömmlichen PD bzw. PID-Reglern mehrere Parameter justiert werden, die sich auch noch wechselseitig beeinflussen. Ausreichende Regeleigenschaften werden dabei oft nur mit einem hohen Verstärkungsfaktor kurz unterhalb der Schwinggrenze erreicht. Die PD/PID-Regelung droht dann bei geringen Veränderungen der Umgebungsbedingungen in die Instabilität abzugleiten. Das neue Regelprinzip ist wesentlich robuster, die Einstellung bei der Wartung oder Inbetriebnahme ist einfacher und schneller durchführbar.

c) Wenn externe Störeinflüsse plötzlich die Geschwindigkeit (Figur 8) oder die Lage (Figur 9) verändern, stellt sich der Regler unverzüglich auf die veränderte Situation ein und führt wieder einen linearen Verlauf des Motor-Stromes herbei, der sicher zum Ziel führt. Auf Störungen, die lange vor dem Ankunftszeitpunkt liegen, wird relativ sanft reagiert, da die gesamte Restzeit von ta zum Ausregeln ausgeschöpft wird. Gleichgroße Störungen kurz vor der Ankunft führen dagegen zu heftigen Reaktionen des Motor-Stromes, um die Störung noch rechtzeitig zu kompensieren. Solange die physikalischen Systemgrenzen (z.B. maximales Motor-Drehmoment) nicht überschritten werden, erreicht die Last ihr Ziel trotzdem ohne Überschwingen und ohne daß sich die Ankunftszeit verzögert. Dies ist ein entscheidender Vorteil gegenüber klassischen Reglern (z.B. PD-Reglern), bei denen sich die Ankunftszeit mit jeder Störung nach hinten verschiebt und bei denen die Ankunftszeit daher nicht genau vorhergesagt werden kann.

d) Wenn das Ziel mit einer bestimmten Geschwindigkeit überfahren werden soll (Vsoll#0), gelingt es dem Regelalgorithmus, gleichzeitig mit dem Ablauf von ta sowohl die gewünschte Endgeschwindigkeit Vsoll als auch die gewünschte Zielposition Ssoll zu erreichen (Figur 10). Dabei ist es nicht erforderlich, daß die Bewegung aus dem Stillstand startet (vgl. Figur 11), und es werden auch negative Geschwindigkeiten oder Wegstrecken richtig verarbeitet, selbst dann, wenn der Endpunkt einer positiven Wegstrecke mit einer negativen Geschwindigkeit (rückwärts) überfahren werden soll (vgl. Figur 12).
 

(9)

(10)

a) k2=0. Damit wird eine annähernd konstante Beschleunigung der Last bewirkt, die dann genau beim Ablauf von ta die Zielposition kreuzt. Gleichung (10) vereinfacht sich in diesem Spezialfall zu:

(11)

Dabei zeigt die Geschwindigkeit einen linearen Verlauf (Figur 13). Dies kann ausgenutzt werden, um das dreiecksförmige Geschwindigkeitsprofil gemäß Figur 3 zu realisieren. Das ist trotz der ungünstigen Verlustleistung (s.o.) dann vorteilhaft, wenn eine hohe Maximalgeschwindigkeit in der Bewegungsmitte gefordert ist oder wenn die gleichmäßige Beschleunigung wünschenswert ist. Dazu wird in der Beschleunigungsphase während des ersten Teils der Bewegung nach Gleichung (11) geregelt, wobei das Ziel Ssolll, z.B. auf den halben Gesamtweg und die Ankunftszeit ta z.B. auf die halbe Gesamtzeit einzustellen ist. Anschließend wird für die Bremsphase auf Gleichung (4) umgeschaltet und mit dem Gesamtweg Ssoll und dem Rest der Gesamtzeit für ta gerechnet. Die Aufteilung in eine Beschleunigungs- und Bremsphase wird bereits in der US 4694229 vorgeschlagen, allerdings wird dort ein ungünstigerer Regelalgorithmus benutzt, bei dem die Ankunftszeit nicht exakt vorhersagbar ist.

b) k2= -k1/ta. Die Beschleunigung und der Motorstrom, die damit eingestellt werden, nehmen linear ab und verschwinden mit Ablauf von ta (aLast(ta)=0, vgl. Gleichung (3)). Den Verlauf zeigt Figur 14.

Gleichung (10) vereinfacht sich in diesem Fall zu:

(12)

Anwendungen ergeben sich, wenn auf die Last zur Ankunftszeit keine Beschleunigungskraft einwirken darf oder wenn noch kurz vor dem Ziel mit äußeren Störeinflüssen zu rechnen ist, zu deren Ausregelung das volle Motor-Drehmoment zur Verfügung stehen soll. Außerdem errechnet sich wieder ein um 25% geringerer Energieverlust gegenüber einer Regelung nach Gleichung (11).